Introducción
Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones.
Los métodos de igualación, sustitución y reducción consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas facil, ¿no?).
A estas ecuaciones, con solo una incognita, se llega a traves de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas.
Método de reducción
Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número de incognitas hasta llegar a ecuaciones con solo una incognita.
Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de la ecuación por dicho número.
Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho ( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las ecuaciones que se suman.
Ejemplo
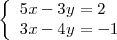
Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones
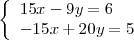
El sumar ambas ecuaciones nos da la ecuación
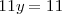
que es una ecuación con una sola incognita y cuya solución es
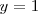
La elección de los factores 3 y -5 se ha hecho precisamente para que la  desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
 desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
Sutituyendo 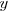 por uno en la primera ecuación del sistema de ecuaciones de partida, se obtiene
por uno en la primera ecuación del sistema de ecuaciones de partida, se obtiene
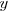 por uno en la primera ecuación del sistema de ecuaciones de partida, se obtiene
por uno en la primera ecuación del sistema de ecuaciones de partida, se obtiene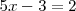
que es otra ecuación con una sola incognita y cuya solución es 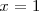 .
.
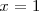 .
.Texto en negrita'Texto en cursiva
Método de igualación
El método de igualación consiste en lo siguiente:
Supongamos que tenemos dos ecuaciones:
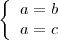
donde  ,
, 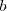 , y
, y  representan simplemente los miembros de estas ecuaciones ( son expresiones algebraicas ).
representan simplemente los miembros de estas ecuaciones ( son expresiones algebraicas ).
 ,
, 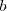 , y
, y  representan simplemente los miembros de estas ecuaciones ( son expresiones algebraicas ).
representan simplemente los miembros de estas ecuaciones ( son expresiones algebraicas ).
De las dos igualdades anteriores se deduce que
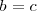
Si resulta que una incognita del sistema de ecuaciones no aparece ni en  ni en
ni en 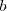 , entonces la ecuación
, entonces la ecuación
 ni en
ni en 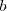 , entonces la ecuación
, entonces la ecuación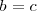
no contendría dicha incognita.
Este proceso de eliminación de incognitas se puede repetir varias veces hasta llegar a una ecuación con solo una incognita, digamos  .
.
 .
.
Una vez que se obtiene la solución de esta ecuación se sustituye  por su solución en otras ecuaciones dode aparezca
por su solución en otras ecuaciones dode aparezca  para reducir el número de incognitas en dichas ecuaciones.
para reducir el número de incognitas en dichas ecuaciones.
 por su solución en otras ecuaciones dode aparezca
por su solución en otras ecuaciones dode aparezca  para reducir el número de incognitas en dichas ecuaciones.
para reducir el número de incognitas en dichas ecuaciones.Ejemplo
El sistema de ecuaciones
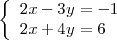
es equivalente a este otro
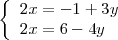
El segundo sistema lo he obtenido pasando los terminos en  del miembro de la izquierda al miembro de la derecha en cada una de las ecuaciones del primer sistema.
del miembro de la izquierda al miembro de la derecha en cada una de las ecuaciones del primer sistema.
 del miembro de la izquierda al miembro de la derecha en cada una de las ecuaciones del primer sistema.
del miembro de la izquierda al miembro de la derecha en cada una de las ecuaciones del primer sistema.
Del segundo sistema se deduce que
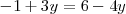
que es una ecuación con una sola incognita cuya solución es 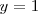 .
.
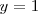 .
.
Sustituyendo  por 1 en la primera ecuación del sistema de partida se tiene que
por 1 en la primera ecuación del sistema de partida se tiene que
 por 1 en la primera ecuación del sistema de partida se tiene que
por 1 en la primera ecuación del sistema de partida se tiene que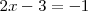
que es una ecuación con una sola incognita y cuya solución es 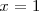 .
.
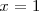 .
.Método de sustitución
Supongamos que un sistema de ecuaciones se puede poner de la forma
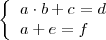
Entonces podemos despejar  en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
 en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
en la segunda ecuación y sustituirla en la primera, para obtener la ecuación: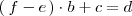
Lo que se busca es que esta ecuación dependa de menos incognitas que las de partida.
Aqui 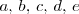 y
y 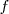 son expresiones algebraicas de las incognitas del sistema.
son expresiones algebraicas de las incognitas del sistema.
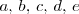 y
y 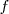 son expresiones algebraicas de las incognitas del sistema.
son expresiones algebraicas de las incognitas del sistema.Ejemplo
Intentemos resolver
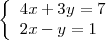
La primera ecuación se puede reescribir de la forma
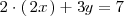
Por otra parte, de la segunda ecuación del sistema se deduce que
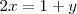
Sustituyendo 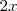 por
por 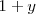 en
en
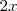 por
por 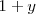 en
en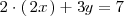
se tiene que
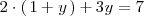
que es una ecuación con solo una incognita y cuya solución es 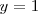 .
.
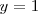 .
.
Sustituyendo  por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
 por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita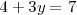
cuya solución es 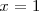 .
.
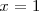 .
.





0 comentarios:
Publicar un comentario